Uniform Cost Search adalah algoritma
terbaik untuk masalah pencarian, yang tidak melibatkan penggunaan heuristik.
Hal ini dapat memecahkan grafik umum untuk biaya yang optimal. Uniform Cost Search kedengarannya pencarian di cabang yang kurang lebih sama dalam biaya.
Uniform Cost Search lagi menuntut penggunaan
antrian prioritas. Ingat bahwa cari pertama kedalaman menggunakan antrian
prioritas dengan kedalaman upto node tertentu menjadi prioritas dan jalur dari
akar ke simpul menjadi elemen yang tersimpan. Antrian prioritas yang digunakan
di sini adalah sama dengan prioritas menjadi biaya kumulatif upto node. Berbeda
cari pertama kedalaman dimana kedalaman maksimum memiliki prioritas maksimum,
Uniform Cost Search memberikan biaya kumulatif minimum prioritas maksimal.
Pencarian dengan Breadth First Search akan menjadi
optimal ketika nilai pada semua path adalah sama. Dengan sedikit perluasan, dapat
ditemukan sebuah algoritma yang optimal dengan melihat kepada nilai tiap path
di antara node-node yang ada. Selain menjalankan fungsi algoritma Breadth First Search,
Uniform Cost Search melakukan ekspansi node dengan nilai path yang paling
kecil. Hal ini bisa dilakukan dengan membuat antrian pada successor yang ada
berdasar kepada nilai path-nya (node disimpan dalam bentuk priority queue).
Proses ekspansi pada Uniform Cost Search dihitung
berdasarkan nilai lintasan g(n) sehingga proses akan berjalan sebagai berikut:
f = {S};
f = {C, A, K}; // 1, 2, 2
f = {A, K, D}; // 2, 2, 2
f = {K, D, B}; // 2, 2, 4
f = {D, L, B}; // 2, 3, 4
f = {L, E, B}; // 3, 3, 4
f = {E, B}; // 3, 4
f = {B, F}; // 4, 4
f = {F, H, G}; // 4, 6, 7
f = {G, H, G}; // 5, 6, 7
f = {H, G}; // 6, 7
Proses eksplorasi node
dimulai dari S sebagai initial state. Eksplorasi node dari S akan menuju ke A,
C, K sebagai successornya. Pada simulasi eksplorasi di atas, untuk mempermudah
proses eksplorasi maka dituliskan dengan C, A, K karena urutannya dituliskan
secara ascending dari nilai g(n) terkecil sehingga akan dihasilkan urutan node
yang akan dieksplorasi selanjutnya. Pada eksplorasi node selanjutnya, nilai
g(n) diakumulasikan dari node awal sampai pada node current yang baru
dieksplorasikan.
Dari proses di atas,
maka dihasilkan jumlah ekspansi node sebanyak 10 kali, dan path yang dilalui
dengan menggunakan algoritma Uniform Cost Search adalah S-C-D-E-F-G.
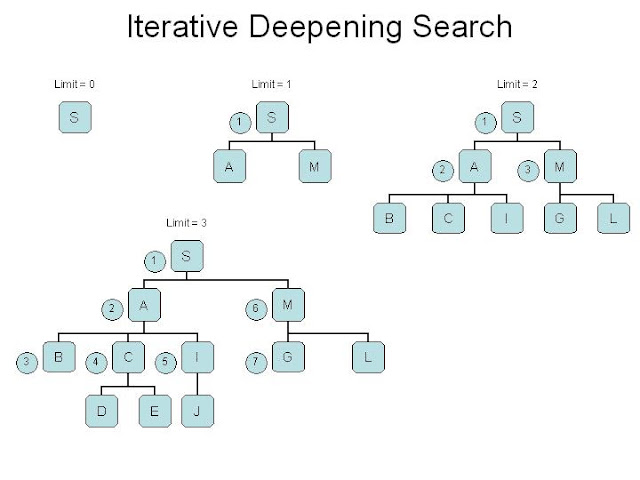
Iterative Deepening Search
Iterative Deepening Search (IDS) adalah pencarian ruang strategi di mana
pencarian mendalam terbatas dijalankan berulang kali, meningkatkan batas
kedalaman dengan setiap iterasi sampai mencapai, kedalaman negara tujuan
dangkal. Iterative Deepening Search setara dengan luas-pertama pencarian,
tetapi menggunakan memori lebih sedikit. Pada setiap iterasi, ia mengunjungi
node dalam pohon pencarian dalam urutan yang sama seperti depth-first search,
tapi urutan kumulatif di mana node pertama kali mengunjungi secara efektif
luasnya pertama. Iterative Deepening Search merupakan metode yang menggabungkan
kelebihan Breadth First Search (Complete dan Optimal) dengan kelebihan Depth
First Search (space complexity rendah atau membutuhkan sedikit memori). Tetapi
konsekwensinya adalah time complexitynya menjadi tinggi.
Iterative Deepening Search menggabungkan depth-first pencari ruang
efisiensi dan kelengkapan luas-pertama pencarian ini (ketika faktor percabangan
terbatas). Ini adalah optimal ketika biaya jalan adalah fungsi non-penurunan
kedalaman node. Kompleksitas ruang Iterative Deepening
Search
adalah, di mana merupakan faktor percabangan dan kedalaman dangkal gawang.
Karena berulang memperdalam kunjungan menyatakan beberapa kali, hal itu mungkin
tampak sia-sia, tapi ternyata menjadi tidak begitu mahal, karena di pohon
sebagian besar node berada di tingkat bawah, sehingga tidak terlalu menjadi
masalah jika tingkat atas yang dikunjungi beberapa kali.
Keuntungan utama dari Iterative Deepening Search dalam mencari permainan pohon
adalah bahwa pencarian sebelumnya cenderung meningkatkan heuristik yang biasa
digunakan, seperti heuristik pembunuh dan pemangkasan alpha-beta, sehingga
perkiraan yang lebih akurat dari skor berbagai node pada pencarian kedalaman
akhir dapat terjadi, dan pencarian selesai lebih cepat karena dilakukan dalam
urutan yang lebih baik. Misalnya, alpha-beta pemangkasan yang paling efisien
jika ia mencari langkah terbaik pertama.
Iterative
Deepening
Expanded
Queue
L=1 S
[<S>]
L=2 S
[<S>]
A
[<A,S> <M,S>]
M
[<M,S>]
L=3 S
[<S>]
A
[<A,S> <M,S>]
B
[<B,A,S> <C,A,S> <I,A,S> <M,S>]
C
[<C,A,S> <I,A,S> <M,S>]
I
[<I,A,S> <M,S>]
M
[<M,S>]
G
[<G,M,S> <L,M,S>]
goal reached!
|